The Problem
On an n x n chessboard, a knight starts at the cell (row, column) and attempts to make exactly k moves.
The rows and columns are 0-indexed, so the top-left cell is (0, 0), and the bottom-right cell is (n - 1, n - 1).
A chess knight has eight possible moves it can make, as illustrated below. Each move is two cells in a cardinal direction, then one cell in an orthogonal direction.

Each time the knight is to move, it chooses one of eight possible moves uniformly at random (even if the piece would go off the chessboard) and moves there.
The knight continues moving until it has made exactly k moves or has moved off the chessboard.
Return the probability that the knight remains on the board after it has stopped moving.
The First Solution
The first solution presented on LeetCode for this problem is available below, which uses several iterators to store probabilities within differnt arrays. We can significantly simplify this solution however through the use of recursion and the Law of Total Probability.
class Solution:
def knightProbability(self, n: int, k: int, row: int, column: int) -> float:
# Possible moves of knight in (row, col) directions
moves = [(2, 1), (2, -1), (-2, 1), (-2, -1), (1, 2), (1, -2), (-1, 2), (-1, -2)]
# Create a 2D memo table to store the probabilities for the current move and the previous move
# We only need to keep track of the probabilities for the current and previous moves
memo = [[0] * n for _ in range(n)]
# Initialize the memo table for the first move with all probabilities set to 1
for i in range(n):
for j in range(n):
memo[i][j] = 1
# For each move from 1 to k
for m in range(1, k+1):
# Create a new 2D memo table to store the probabilities for the current move
new_memo = [[0] * n for _ in range(n)]
# For each cell on the board
for i in range(n):
for j in range(n):
prob = 0
# Iterate over all possible moves from the previous cell
for move in moves:
new_i = i + move[0]
new_j = j + move[1]
# If the move is still on the board
if 0 <= new_i < n and 0 <= new_j < n:
prob += memo[new_i][new_j]
# Update the probability of the current cell for current moves
new_memo[i][j] = prob / 8
# Set the memo table for the previous move to the memo table for the current move
memo = new_memo
# Return the probability of the starting cell for k moves
return memo[row][column]The Law of Total Probability
Suppose the events are mutally exclusive and exhaustive events in a sample space, then for any event in that sample space:
If we consider the knight starts within the red (4, 4) board below, and only has 1 move, then only will 3 out of the 8 possible moves keep the knight within the board.
If we consider this first example, we can manually set out the numbers to visualise the problem before writing a general solution.
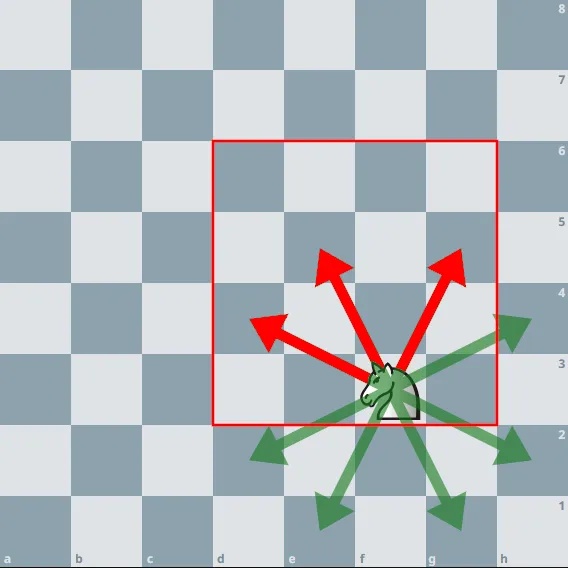
With an array containing the probability of each move occurring, [0.125, 0.125, 0.125, 0.125, 0.125, 0.125, 0.125, 0.125], and another array of the probabilities that the knight stays on the board, [1, 1, 1, 0, 0, 0, 0, 0], we can calculate the result through the sum of both arrays.
The law of total probability sums the conditional probabilities of all cases, multiplied by the probability of each case occurring:
(0.125 * 1) + (0.125 * 1) + (0.125 * 1) + (0.125 * 0) + (0.125 * 0) + (0.125 * 0) + (0.125 * 0) + (0.125 * 0) = 0.375
We were able to set the probability that the knight would remain on the board to as it was the final move of the knight - if the knight ends on a square within the board there is a chance the knight has remained within the board. Things start to get a bit more complicated after one move, as there is no guarantee the knight will remain within the board after the first move.
Let’s consider the previous example but where the knight moves twice instead of just once. We can work through this problem backwards to understand how the statistics behind the solution works.
For each of the 3 possibilities the knight can make for it’s second move, we can calculate the probability that the knight stays within the board like we did in the previous example, as it is the final move.
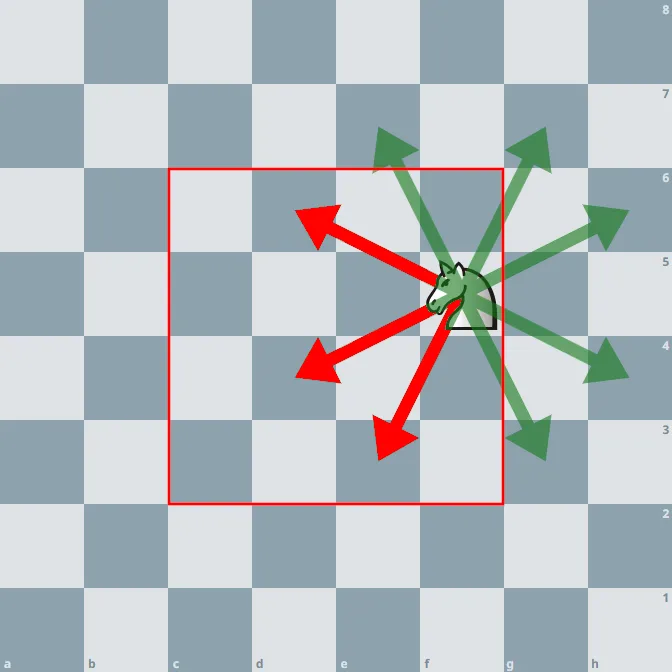
(0.125 * 1) + (0.125 * 1) + (0.125 * 1) + (0.125 * 0) + (0.125 * 0) + (0.125 * 0) + (0.125 * 0) + (0.125 * 0) = 0.375
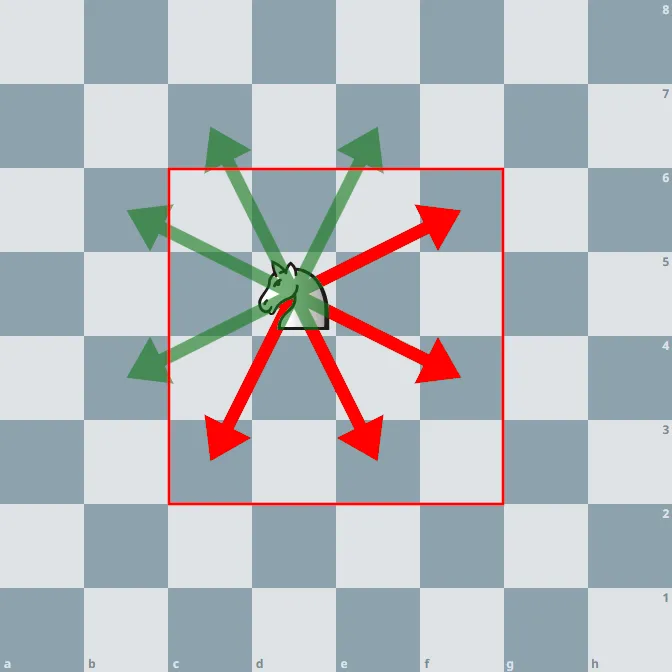
(0.125 * 1) + (0.125 * 1) + (0.125 * 1) + (0.125 * 1) + (0.125 * 0) + (0.125 * 0) + (0.125 * 0) + (0.125 * 0) = 0.5
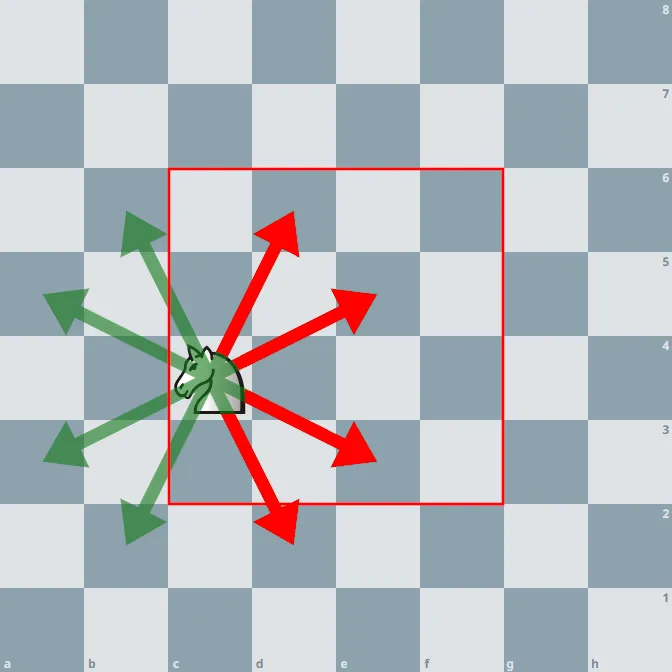
(0.125 * 1) + (0.125 * 1) + (0.125 * 1) + (0.125 * 0) + (0.125 * 0) + (0.125 * 0) + (0.125 * 0) + (0.125 * 0) = 0.375
We can plug these results back into the original equation to determine the final probability:
(0.125 * 0.375) + (0.125 * 0.500) + (0.125 * 0.375) + (0.125 * 0.000) + (0.125 * 0.000) + (0.125 * 0.000) + (0.125 * 0.000) + (0.125 * 0.000) = 0.15625
The Solution
The following solution uses the law of total probability to calculate the final answer
class Solution:
def knightProbability(n: int, k: int, row: int, column: int) -> float:
MOVES = [(2, 1), (2, -1), (-2, 1), (-2, -1), (1, 2), (1, -2), (-1, 2), (-1, -2)]
def dp(i, j, k):
# check knight within board
if not (0 <= i < n and 0 <= j < n):
return 0
# check moves left remaining
if k == 0:
return 1
return sum(1/8 * dp(i + x, j + y, k - 1) for x, y in MOVES)
return dp(row, column, k)